18.圆等腰 角分线 二倍角解三角形

.

圆等腰 角分线 二倍角解三角形

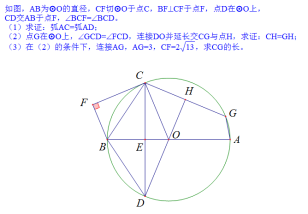
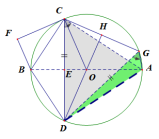
第一问探究：

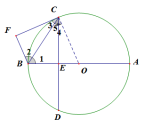
等弧=>垂径定理基本图形=>∠CEB=90°，又∵∠F=90°，∠3=∠5=>∠2=∠1，

寻找中间过渡角，

辅助线：连半径，①切线基本图形，∠FCO=90°，∠F=90°，

=>FB∥CO，（平行）∴∠2=∠4。

②造等腰，∠1=∠4。

①②=>∠2=∠1，（角平分线）

基本图形：平行+等腰=>角平分线

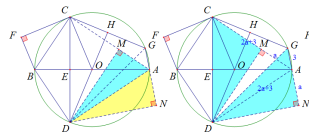
第二问探究：

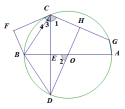
分弦=>垂径定理基本图形=>∠CHD=90°，又∵CE⊥AB，=>∠1=∠2（过渡角），

∠4与∠2不能直接有联系，故寻找第二过渡角，∠2=2∠3，又∵∠4=2∠3，∴∠2=∠4。

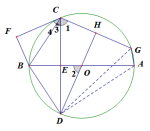
第三问的探究：

基本图形关键词：①圆等腰 角分线

②SSA结构，作双垂

③圆内接对角互补型四边形之一，含等腰，角分线

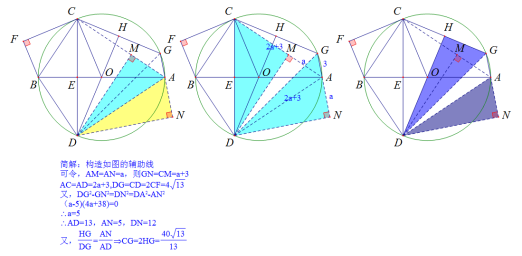
特殊解三角形，已知两边及两内角二倍角关系，内构：二倍角。

.

设∠FCB=α，易知∠DGA=90°-α，∠GAD=180°-2α，则∠GAD=2∠DGA。

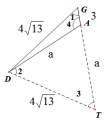子母型相似，求a值。

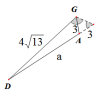子母型相似，求a值。

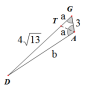子母型相似，

.