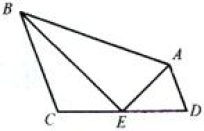
7.截长补短

截长补短

.

.

.

模型 截长补短

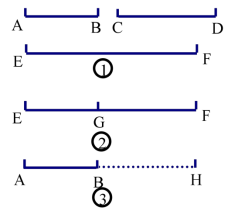
如图①，若证明线段 AB、CD、EF 之间存在

EF=AB+CD，可以考虑截长补短法。

截长法：如图②，在 EF 上截取 EG=AB，再证明

GF=CD 即可。

补短法：如图③，延长 AB 至 H 点，使 BH=CD，

再证明 AH=EF 即可。

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

模型分析

截长补短的方法适用于求证线段的和差倍分关系。截长，指在长线段中截取一段等于已知线段；补短，指将短线段延长，延长部分等于已知线段。

该类题目中常出现等腰三角形、角平分线等关键词句，可以采用截长补短法构造全等三角形来完成证明过程。

.

.

.

.

.

.

.

.

.

.

模型实例

例 1．如图，已知在△ABC中，∠C=2∠B，AD平分∠BAC 交 BC 于点 D。

求证：AB=AC+CD。

.

.

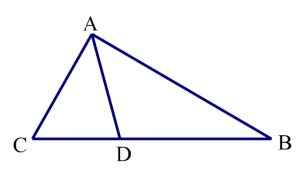
证明：如图在AB上取一点E使AE=AC

∵AD平分∠BAC

∴∠CAD=∠DAE,AD=AD

∴△CAD≌△EAD

∴CD=ED,∠C=∠AED=∠B+∠EDB

又∠C=2∠B

∴∠B=∠EDB

∴ED=EB

∴AB=AE+EB=AC+CD

∴AB=AC+CD

.

.

.

.

.

.

.

.

.

.

.

.

.

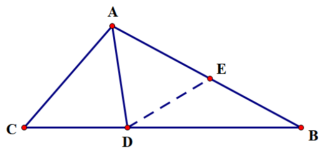
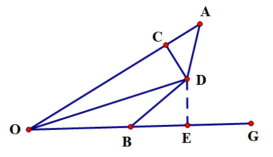
例 2．如图，已知 OD 平分∠AOB，DC⊥OA 于点 C，∠A=∠GBD。

求证：AO+BO=2CO。

.

.

.

.

.

.

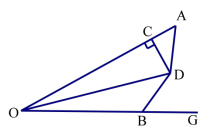
证明：如图过D点作DE垂直BG交于点E

∵ OD 平分∠AOB，DC⊥OA 于点 C

∴DC=DE，∠COD=∠DOE,OD=OD

∴△OCD≌△OED

∴OC=OE

又∠A=∠GBD,DC=DE

∴RT△DCA≌RT△DEB

∴AC=BE

∴AO+BO=AC+CO+EO-BE=CO+OE=2OC

∴AO+BO=2CO

.

.

.

.

.

.

.

.

.

.

模型练习

.

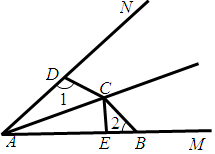
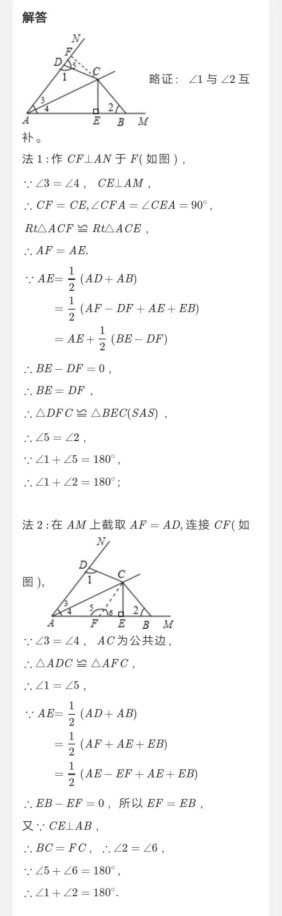
1.如图，已知点C是∠MAN的平分线上一点，CE⊥AB于E，B、D分别在AM、AN上，且AE=（AD+AB）.问：∠1和∠2有何关系.

.

.

.

2.如图，已知△ABC中，∠A＝90°，AB＝AC，BE平分∠ABC，CE⊥BD于E，求证：CE=BD.

.

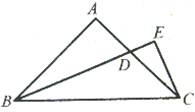
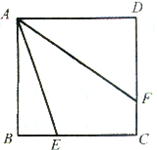
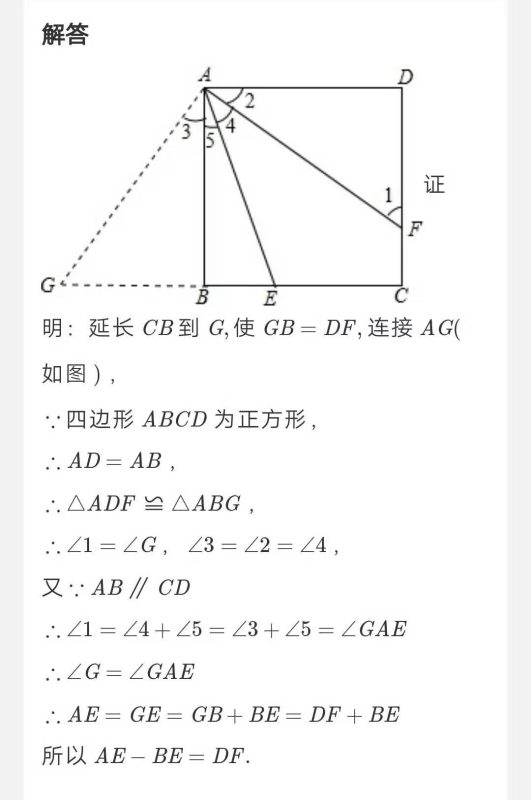
3. 如图，已知正方形ABCD中，E为BC边上任意一点，AF平分∠DAE．求证：AE－BE＝DF．

.

.

.

.

.

.

.

.

.

4.如图，已知四边形ABCD中，AD∥BC，若∠DAB的平分线AE交CD于E，连结BE，且BE恰好平分∠ABC，判断AB的长与AD＋BC的大小关系并证明.

.

.

.

.

.

.

.

.

.