5.角平分线+垂直构造等腰三角形
角平分线模型
模型 3 角平分线+垂线构造等腰三角形
如图，P 是∠MON 的平分线上一点，AP⊥OP 于 P 点，延长 AP交ON于点 B。
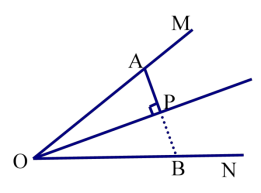结论：△AOB 是等腰三角形。
模型证明：
由已知可得AP⊥OP,BP⊥OP,OP=OP,∠POA=∠POB
∴△POA≌△POB
∴OA=OB
∴△AOB 是等腰三角形
模型分析
构造此模型可以利用等腰三角形的“三线合一”，也可以得到两个全等
的直角三角形，进而得到对应边、对应角相等。这个模型巧妙地把角平分线
和三线合一联系了起来。
模型实例
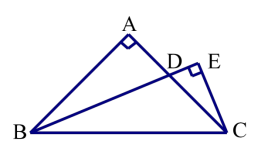
如图，已知等腰直角三角形 ABC 中，∠A=90°，AB=AC，BD 平分∠ABC，
CE⊥BD，垂足为 E。求证：BD=2CE。
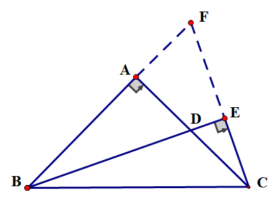
证明：如图延长BA、CE交于点F则有：
∠ABE=∠CBE，BE=BE
∴RT△BEF≌RT△BEC
∴CE=EF
∴CF=2CE
又∵∠ADB=∠CDE
∠DCE+∠CDE=∠DCE+∠F=90°
∴∠ADB=∠F
又AB=AC
∴RT△BAD≌RT△CAF
∴BD=CF
∴BD=2CE.
模型练习
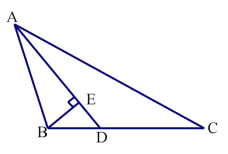
1．如图，在△ABC 中，BE 是角平分线，AD⊥BE，垂足为 D。
求证：∠2=∠1+∠C。
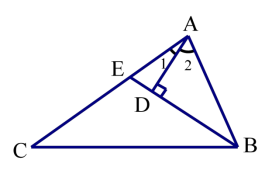
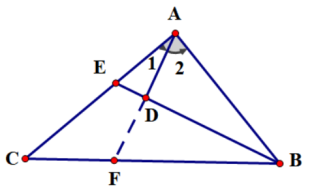
证明：如图延长AD交BC于点F则有
BD=BD，∠ABD=∠FBD
∴RT△ADB≌RT△FDB
∴∠2=∠BFD=∠1+∠C
∴∠2=∠1+∠C
2．如图，在△ABC 中，∠ABC=3∠C，AD 是∠BAC 的角平分线，BE⊥AD 于点 E。
求证：BE= ½（AC-AB）。
