3.角平分线的四大模型,角平分线上的点向两边作垂线.
3、角平分线的四大模型
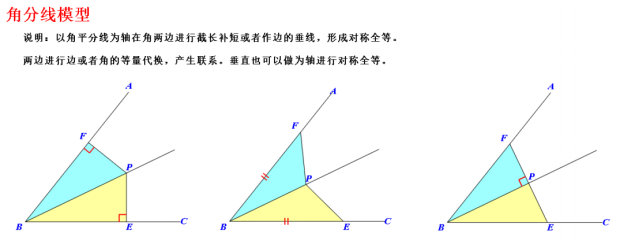
模型 1 :角平分线上的点向两边作垂线
如图,P 是∠MON 的平分线上一点,过点 P 作 PA⊥OM 于点 A,PB⊥ON 于点 B。
结论:PB=PA。 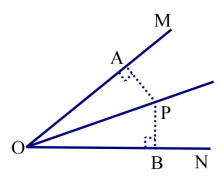
模型证明:
∵OP平分∠MON,
∴∠AOP=∠BOP;
又 PA⊥OM ,PB⊥ON,
∴∠OAP=∠OBP=90°;
OP=OP;
∴RT△OAP≌RT△OBP,
∴PB=PA。
模型分析
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,
为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的
突破口。
模型实例
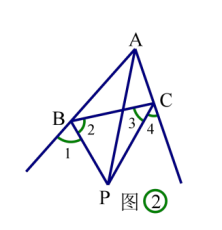
(1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB,BC=6,BD=4,那么点 D
到直线 AB 的距离是_____;
(2)如图②,∠1=∠2,∠3=∠4。
求证:AP 平分∠BAC。
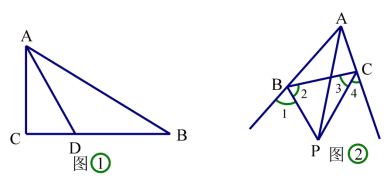
解析:(1)由角平分线模型知,D到AB的距离等于DC=2
(2)如图分别做AB、BC、AC三边的高,由题意易得三边高相等,
∴AP 平分∠BAC
模型练习
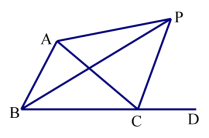
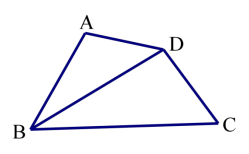
1.如图,在四边形 ABCD 中,BC>AB,AD=DC,BD 平分∠ABC。 求证:∠BAD+∠BCD=180°。
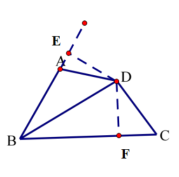
证明:如图延长BA,
过D作DE、DF垂直BA延长线、BC于E、F两点,
∵BD 平分∠ABC
∴DE=DF,
又AD=DC
∴RT△DEA≌RT△DFC
∴∠DAE=∠BCD
∴∠BAD+∠BCD=180°
2.如图,△ABC 的外角∠ACD 的平分线 CP 与内角∠ABC 的平分线 BP 交于点P,若∠BPC=40°,则∠CAP=——。