21.定角夹定高（探照灯模型）

定角夹定高（探照灯模型）

什么叫定角定高，如右图，直线BC外一点A，A到直线BC距离为定值（定高），∠BAC为定角。则AD有最小值。又因为，像探照灯一样所以也叫探照灯模型。

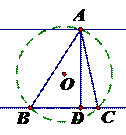
我们可以先看一下下面这张动图，在三角形ABC当中，∠BAC是一个定角，过A点作BC边的高线，交BC边与D点，高AD为定值。

从动态图中（如图定角定高1.gsp）我们可以看到，如果顶角和高，都为定值，那么三角形ABC的外接圆的大小，也就是半径，是会随着A点的运动而发生变化的。从而弦BC的长也会发生变化，它会有一个最小值，由于它的高AD是定值，因此三角形ABC的面积就有一个最小值。

我们可以先猜想一下，AD过圆心的时候，这个外接圆是最小的，也就是，BC的长是最小的，从而三角形ABC的面积也是最小的。

（定长可用圆处理，特别，定长作为高可用两条平行线处理）

那么该如何证明呢？

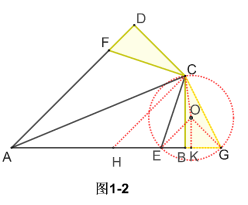
首先我们连接OA,OB,OC。过O点作OH⊥BC于H点.（如图1）

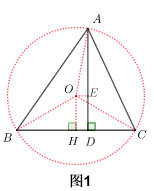
显然OA+OH≥AD，当且仅当A,O,D三点共线时取“=”。由于∠BAC的大小是一个定值，而且它是圆o的圆周角，因此它所对的圆心角∠AOB的度数，也是一个定值。

因此OH和圆O的半径，有一个固定关系，所以，OA+OH也和$\odot O$的半径，有一个固定的等量关系。再根据我们刚才说的，OA+OH$\ge$AD，就可以求得圆O半径的最小值。

[简证：OA+OH$\ge$AD

OEDH为矩形，OH=ED，在Rt△AOE中，AO>AE，∴AO+OH=AO+ED>AE+ED=AD]

.

下面我们根据一道例题来说明它的应用。

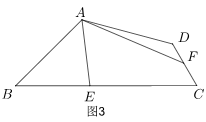
例：如图，在四边形ABCD中，AB=AD=CD=4，AD∥BC，∠B=60°，点E、F分别为边BC、CD上的两个动点，且∠EAF=60°，则△AEF的面积是否存在最小值？若存在，求出其最小值；若不存在，请说明理由。

.

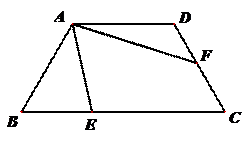
【简答】图中有角含半角模型，因此我们想到旋转的方式来处理.

.

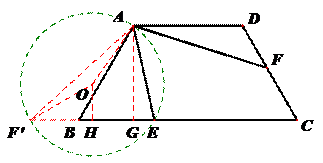
将△ADF绕A点顺时针旋转120°，得△ABF′，则∠EAF′=60°，易证△AEF′≌△AEF，作△AEF′的外接圆⊙O，作OH⊥BC于点H，AG⊥BC于点G，则∠F′OH=60°，AG=$\frac{\sqrt{3}}{2}AB=2\sqrt{3}$，设 ⊙O的半径为r，则OH=$\frac{OF}{2}=\frac{r}{2}$ .

$\because OA+OH\ge AG，\therefore r+\frac{r}{2}\ge 2\sqrt{3}$，$\therefore r\ge \frac{4\sqrt{3}}{3}$

∵∠FAE=∠F’AE=$\frac{1}{2}$∠FOE=60°

∴F’E=$\sqrt{3}r$

$\therefore S_{\Delta AEF}=S_{\Delta AE{F}^{‘}}=\frac{1}{2}\cdot E{F}^{‘}\cdot AG$

$=\frac{1}{2}\times \sqrt{3}r\cdot 2\sqrt{3}\ge 4\sqrt{3}$

∴△AEF的面积最小值为$4\surd 3$

.

以下是两到相关的针对练习题，大家学习完以后可以去自主的完成一项，后面也有详细的解答过程，做完以后大家可以对照一下答案，学会了这种类型题的解法。

解题步骤：

1.作定角定高三角形外接圆，并设外接圆半径为r，用r表示圆心到底边距离及底边长；

2.根据“半径+弦心距$\ge$定高”求r的取值范围；

3.用r表示定角定高三角形面积，用r取值范围求面积最小值。

.

【针对练习】

1.（1）如图1，在△ABC中，∠ACB=60°，CD为AB边上的高，若CD=4，试判断△ABC的面积是否存在最小值？若存在，请求出面积最小值；若不存在，请说明理由.

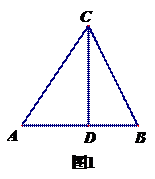
（2）如图2，某园林单位要设计把四边形花圃划分为几个区域种植不同花草。在四边形ABCD中，∠BAD=45°，∠B=∠D=90°，CB=CD=6√2，点E、F分别为边AB、AD上的点，若保持CE⊥CF，那么四边形AECF的面积是否存在最大值，若存在，请求出面积的最大值；若不存在，请说明理由。

.

.

.

.

.

.

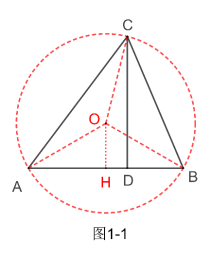
（1）解：如图1-1

作△ABC的外接圆$\odot O$，连OA、OB、OC，作OH⊥AB于H

①设$\odot O$半径为r，则OH=$\frac{1}{2}OA=\frac{1}{2}r$，AB=2AH=2$\times \frac{\sqrt{3}}{2}OA=\sqrt{3}r$

②∵CO+HO$\ge$CD 即r+$\frac{1}{2}r\ge$4 得r$\ge \frac{8}{3}$

③$S_{\Delta ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}\times \sqrt{3}r\times 4=2\sqrt{3}r\ge 2\sqrt{3}\times \frac{8}{3}=\frac{16}{3}\sqrt{3}$

.

（2）分析：此处求面积最大值，而定角定高一般求面积最小值。

由于：

$S_{四边形AECF}=S_{四边形ABCD}-S_{\Delta CDF}-S_{\Delta CBE}$

=$72\sqrt{2}+72-（S_{\Delta CDF}+S_{\Delta CBE}）$

因此，只要$S_{\Delta CDF}+S_{\Delta CBE}$最小，$S_{四边形AECF}$面积最大

.

解：如图1-2所示

在AB上找一点H，使AH=HC。延长AB至G，使BG=FD，连CG，作△CEG的外接圆$\odot O$

①证AC为∠BAD平分线

②求$S_{四边形ABCD}$面积。∠CHB=45°，AH=CH=$\sqrt{2}CB=12$

HB=BC=$6\sqrt{2}$ AB=12+$6\sqrt{2}$

$S_{四边形ABCD}=2S_{\Delta ABC}=2\times \frac{1}{2}AB\cdot BC=AB\cdot BC$

=$\left(12+6\sqrt{2}\right)\times 6\sqrt{2}=72\sqrt{2}+72$

③△CDF≌△CBG，则$S_{\Delta CDF}+S_{\Delta CBE}$=$S_{\Delta CEG}$

④求$S_{\Delta CDF}+S_{\Delta CBE}=S_{\Delta CEG}$最小面积

∠ECG=135°-90°=45°定角，CB=$6\sqrt{2}$定高

Ⅰ.设$\odot O$的半径为r，则EK=OK=$\frac{\sqrt{2}}{2}OE=\frac{\sqrt{2}}{2}r$，EG=2EK=$\sqrt{2}r$

Ⅱ.CO+OK$\ge CB$ 即r+$\frac{\sqrt{2}}{2}r\ge 6\sqrt{2}$ r$\ge 12\sqrt{2}-12$

Ⅲ.$S_{\Delta CEG}=\frac{1}{2}CB\cdot EG=\frac{1}{2}\times 6\sqrt{2}\times \sqrt{2}r=6r\ge 72\sqrt{2}-72$

⑤求$S_{四边形AECF}$的最大值。

$S_{四边形AECF}=S_{四边形ABCD}-S_{\Delta CDF}-S_{\Delta CBE}$

=$72\sqrt{2}+72-（S_{\Delta CDF}+S_{\Delta CBE}）$

$=72\sqrt{2}+72-S_{\Delta CEG}\ge 72\sqrt{2}+72-\left(72\sqrt{2}-72\right)=144$

.

2.已知等边△ABC，点P是其内部一个动点，且AP=10，M、N分别是AB、AC边上的两个动点，求△PMN周长最小时，四边形AMPN面积的最大值.

分析：①△PMN最小值即将军饮马问题。如图2-1。

.

.

.

.

.

.

.

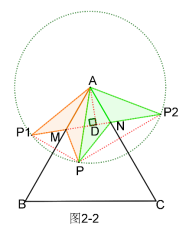②四边形AMPN面积该如何表示？如图2-2

AP=10，则P在以A为圆心10为半径的圆上

由轴对称性可知，$S_{\Delta A{P}_{1}M}=S_{\Delta APM}$，$S_{\Delta {AP}_{2}N}=S_{\Delta APN}$

$S_{四边形AMPN}=S_{\Delta APM}+S_{\Delta APN}=S_{\Delta A{P}_{1}M}+S_{\Delta A{P}_{2}N}$=$S_{\Delta A{P}_1{P}_2}-S_{\Delta AMN}$

∵$S_{\Delta A{P}_1{P}_2}=\frac{1}{2}AD\cdot P_1{P}_2=\frac{1}{2}\left(\frac{1}{2}A{P}_1\right)\cdot \left(\sqrt{3}A{P}_1\right)=\frac{\sqrt{3}}{4}A{P}^2=25\sqrt{3}$

∴只要$S_{\Delta AMN}$最小，则$S_{四边形AMPN}$最大

③$S_{\Delta AMN}$最小，且∠MAN=60°定值，AD=$\frac{1}{2}A{P}_1=\frac{1}{2}AP=5$定值，即定角定高问题

.

解：①求△PMN周长最小。作P关于AB的对称点$P_1$，作P关AC的对称点$P_2$，连$P_1{P}_2$。此时，△PMN周长即为最小（两点之间线段最短）

②四边形AMPN面积表达式。连$A{P}_1、A{P}_2$，过A作AD⊥$P_1{P}_2$

$\because \angle MAP=\angle MA{P}_1，\angle NAP=\angle NA{P}_2，\angle MAN=\angle MAP+\angle NAP=60°$

$\therefore \angle MA{P}_1+\angle NA{P}_2=\angle MAP+\angle NAP=\angle MAN=60°$

$\angle P_{1}A{P}_2=\angle MA{P}_1+\angle MAN+\angle NA{P}_2=120°$

又$AP=A{P}_1=A{P}_2=10$

∴$\angle A{P}_1{P}_2=\angle A{P}_2{P}_1=30°$

AD=$\frac{1}{2}A{P}_1=5$  $P_{1}D=P_{2}D=\frac{\sqrt{3}}{2}A{P}_1=5\sqrt{3}$   $P_1{P}_2=2P_{1}D=10\sqrt{3}$

$S_{\Delta A{P}_1{P}_2}=\frac{1}{2}AD\cdot P_1{P}_2=25\sqrt{3}$

∴$S_{四边形AMPN}=S_{\Delta A{P}_1{P}_2}-S_{\Delta AMN}=25\sqrt{3}-S_{\Delta AMN}$

∴当$S_{\Delta AMN}$最小时，$S_{四边形AMPN}$最大

③求$S_{\Delta AMN}$的最小值。如图2-3

作△AMN的外接圆$\odot O$，连OA、OM、ON，作OH⊥MN于H

Ⅰ.设$\odot O$的半径为r，

则OH=$\frac{1}{2}OM=\frac{1}{2}r$，$MN=2MH=2\times \frac{\sqrt{3}}{2}OM=\sqrt{3}r$

Ⅱ.AO+OH$\ge AD$，即$r+\frac{r}{2}\ge 5$，r$\ge \frac{10}{3}$

Ⅲ.$S_{\Delta AMN}=\frac{1}{2}AD\cdot MN=\frac{1}{2}\times 5\times \sqrt{3}r=\frac{5}{2}\sqrt{3}r\ge \frac{25}{3}\sqrt{3}$

④$S_{四边形AMPN}=S_{\Delta A{P}_1{P}_2}-S_{\Delta AMN}=25\sqrt{3}-S_{\Delta AMN}\le 25\sqrt{3}-\frac{25}{3}\sqrt{3}=\frac{50}{3}\sqrt{3}$

∴四边形AMPN面积最大值为$\frac{50}{3}\sqrt{3}$

这就是我们所说的定价定高类隐形圆的处理方法。相对来说难度还是比较大的，这类题通常会作为中考压轴题出现，如果没有学习过解题方法的话，自己是很难想出来它的做法，希望同学们下去以后多加练习。只要方法掌握了以后，其实也是很容易拿到满分的。

【同类配题】

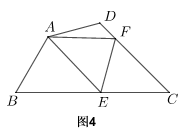
1.如图3，四边形ABCD中，AB=AD=4$\sqrt{2}$，∠B=45°，∠D=135°，点E，F分别是射线CB、CD上的动点，并且∠EAF=∠C=60°，求△AEF的面积的最小值.

 

.

.

.

.

.

.

.

.

.

2.如图4，四边形ABCD中，∠A=135°，∠B=60°，∠D=120°，AD=5，AB=6，E、F分别为边BC及射线CD上的动点，∠EAF=45°，求△AEF面积的最小值.

.

..

.

.

.

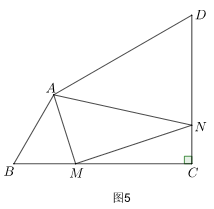
3.如图5，四边形ABCD中，∠B=∠D=60°，∠C=90°，AD=2AB=2，M、N分别在直线BC、CD边上，∠MAN=60°，求△AMN面积最小值.

.

.

.

.

.

.

.

.

.

.

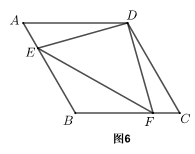
4.如图6，四边形ABCD边长为6的菱形，其中，$\angle A=60°$，E、F分别在射线AB、BC上，∠EDF=90°，求△EDF面积的最小值.