20.矩形大法

“矩形大法”

.

主要从三个方面和大家交流：

一：“矩形大法”的提出背景

二：“矩形大法”的基本构造

三：“矩形大法”的实例应用

一、矩形大法”的提出背景

问题：我们如何刻画一个角大小呢？

是的，角的大小有两种刻画方法：一种是传统的、人人皆知的度数刻画法；另一种是常被我们忽略的边长刻画法（即三角函数值）。

如果两个角的大小是用度数体现的，那么这两个角的和与差的度数能够非常容易地计算出来。

但如果两个角的大小是采用边长（即三角函数值）刻画的，那么两个角的和或差的大小是多少呢？

自然，这两个角和与差的大小也只能采用三角函数值刻画。

也许学习数学的人第一反应是马上想到高中的两角和与差的三角公式。

但现在讨论的背景是初中数学教学因此我们要回避用高中数学知识。

首先要提的就是南通2014年的28题第三问：

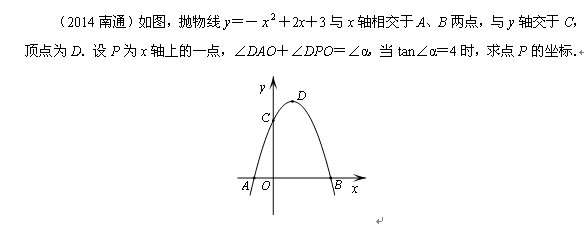
不知大家第一次看到这道题的第一反应是什么？
能否在短时间中用传统方法解决？

看到两角和差关系这样的条件想到什么？

本题它有比较巧妙的求法，但要发现，还是需要一定的时间的。

这里涉及到两角和差关系，需要说明的是，命题人员绝非希望你采用高中“两角和与差的三角公式”去解决问题，这是由于：

⑴他们当初没有意识到采用这样的思考方法是合理的，而且只要方法得当，的确能够解决问题。

⑵即使意识到了，他们认为因为初中不具备这样的知识，有这样的想法却因为不具备的能力，从而无法解决原问题。

⑶最关键的原因是，由于命题人员想出了构思极为巧妙，常人很难想到的解法。

.

于是，这样的考题在不知不觉中出现了，而且通常情况下，这样的考题必定处于试卷中的难题位置．那如果我们能有比较好的方法去破解这个和差关系，那不就可以不花多少时间直接攻破此题了呢！

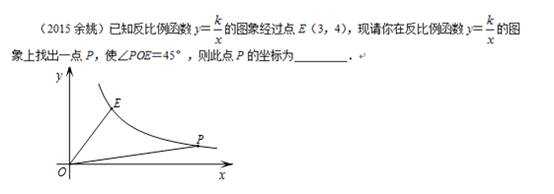
再譬如今年盐城的中考题第3问：

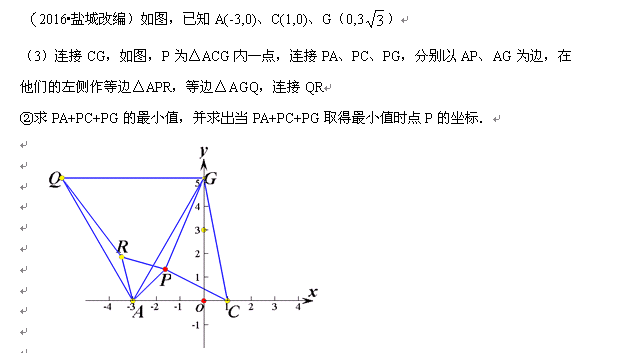
这题给出的答案也比较复杂，我想学生在短时间里容易找到点P的位置却不易求出点P坐标。那么这题究竟如何成功破解呢？

而类似这样的问题不管小题，大题，其实在中考中是比较多的。

现在的问题是，有些题目构思非常巧妙，但采用“因果确定法”思考，面临的困难就是：已知两个角的大小（边长刻画），最后只有在解决了这两个角的和或差的问题后，才能真正解决原问题。

那么有没有既遵从原始的“因果确定法”的思考方法，又付出代价不大，同时还易于操作的解法呢？ 也即如何做到“想有背景，解不超纲”呢？

这就让人开始思考从比值刻画一个角的大小，就得出现一个包含这个锐角的直角三角形。

那么两个角呢？

就必须出现两个直角三角形。

最后还要有两个角的和或差的大小的比值刻画，即出现了第三个角，又必须出现一个含有这个和角或差角的直角三角形。这样就需要三个直角三角形，那么怎样才能沟通彼此联系呢？在平时的基本构图模型中有吗？

在这些想法的基础上，朦朦胧胧地继续探求构造，最后终于产生了那个精妙绝伦的矩形——一下子全部满足了要求！

为了在网络上交流，既有一定的趣味性，又揭示方法的本质，于特将其取名为“矩形大法”。我们在课堂上有时为了表述的方便或激发学生的学习兴趣和积极性，也可以一起命些名称，不必太过计较说法，我的课堂里还有个“晨博公式”呢！（晨博是我现在的一个学生名字）

.

二、 “矩形大法”的基本构造

下面我们以75°，15°这两个特殊角为例聊聊矩形的构造

我们可以通过30°与15°的倍半角关系求出tan15°的值，通过互余关系求出tan75°的值。
那如果利用30°，45°这两角的和差关系又该怎样构图表示出75°与15°的正切值呢？

1、先思考75°即45°与30°和的构造：

.

根据刚才的阐述，我们究竟该如何用比值来刻画45°，30°，以及75°这三个角呢？

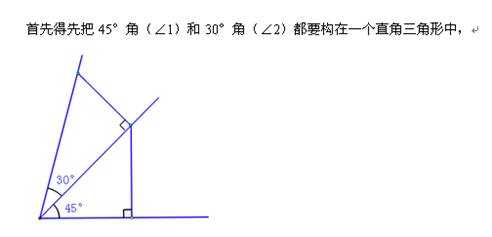
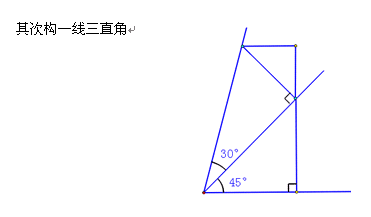
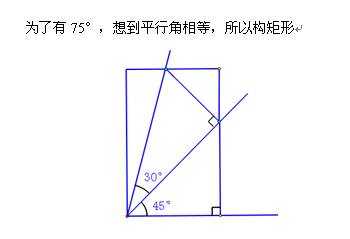
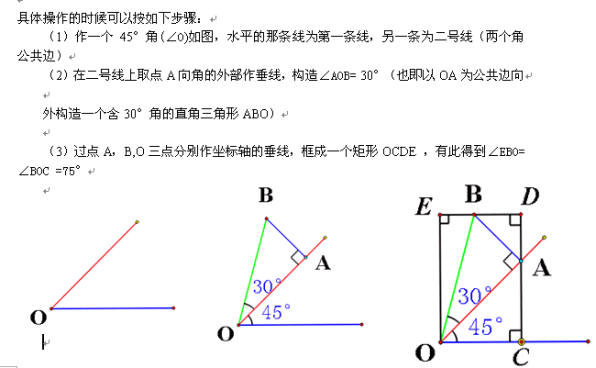
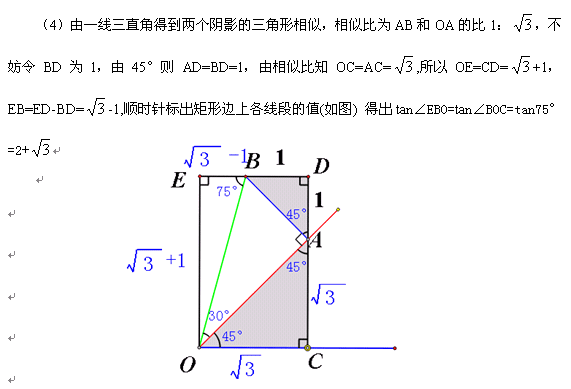
2、15°即45°与30°差的构造

刚才两角和是在一个角的基础上向外“扩张”，现在是两角差，该如何构造呢？

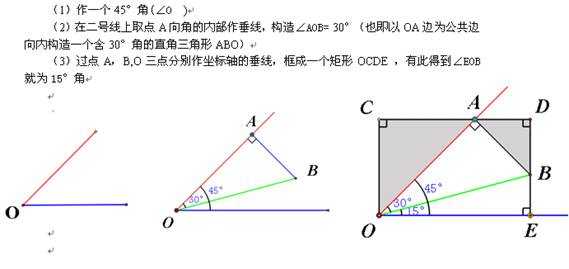
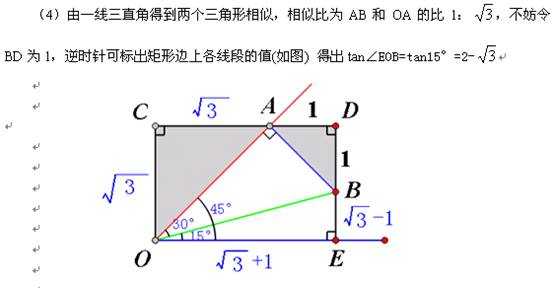
3、已知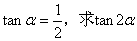 即构图说明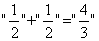

借用上次纪博士讲座中的图：

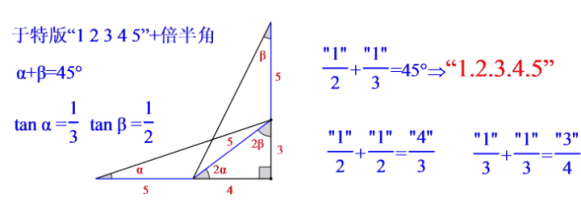
现在如何用矩形构造呢？

【江苏苏晓艺  向外作是求和，向里作是求差】

总结的好！

这里我们可以仿照上面的15°，75°，的构造，得到如下的构图

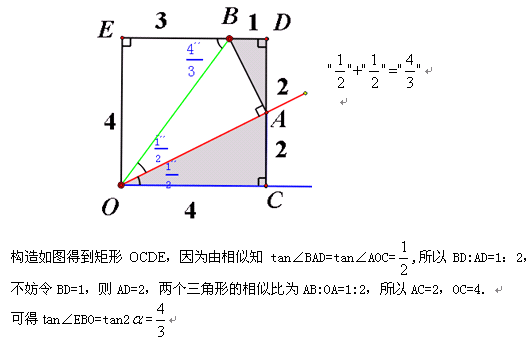
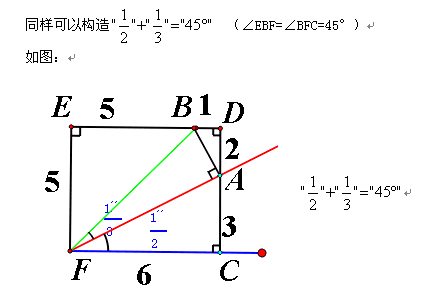
从这里可以看出 “12345”显然可以看成是“矩形大法”的一个特殊运用．
掌握了矩形大法，要解释为什么有：“1/2”＋“1/3”＝45°，“1/2”＋“1/2”＝“4/3”等，就显得非常容易了哦！

其基本步骤是：构直角，框矩形，用相似，表线段。

.

下面先来几个小题，热下手哦！

1、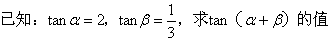

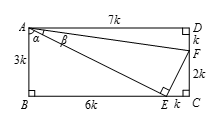
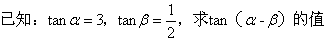
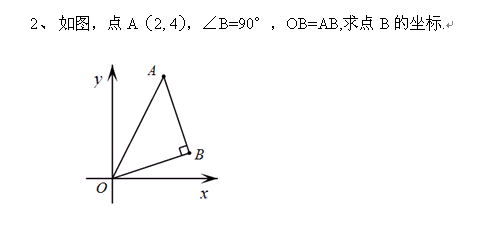
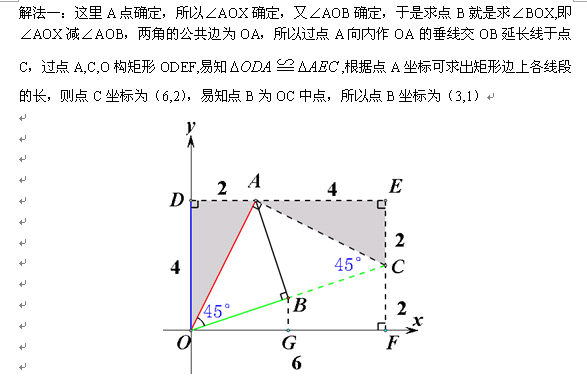
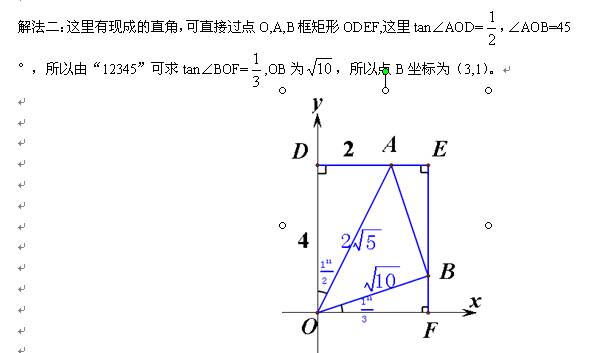
如果是填空或选择的小题，那就可秒了哈

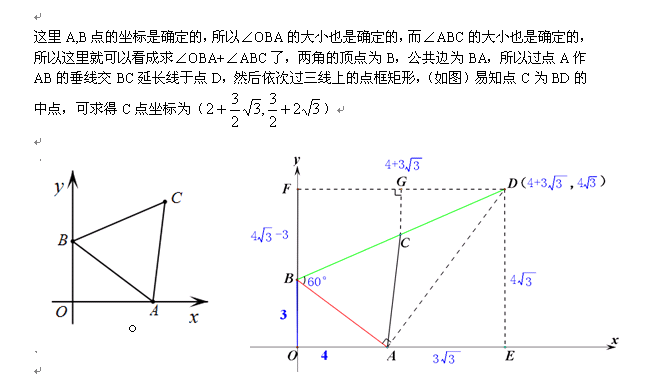
解法二：根据等边三角形的特殊性，作AB边上的高，过垂足构一线三直角框矩形也是比较方便的。

.

4、先来看一道2013淄博中考题的第三问

.

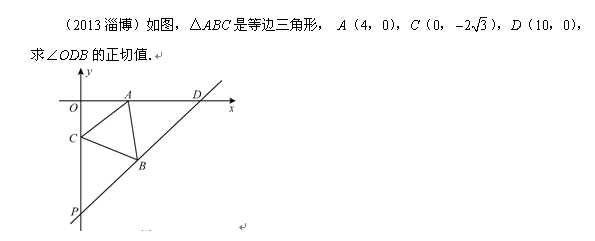
本题中求∠ODB的正切值的关键是什么呢？

本题中求∠ODB的正切值，一边OD确定，所以只要确定点B的坐标即可。这题就和上一个小题一样了。这里既可以看成∠OAC+60°角，也可以是∠OCA+60°角的和差关系，可构如下图：

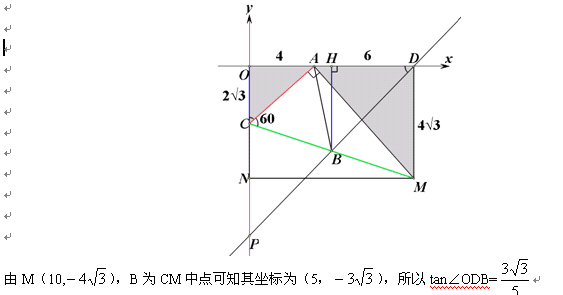
5、再来个中考小题

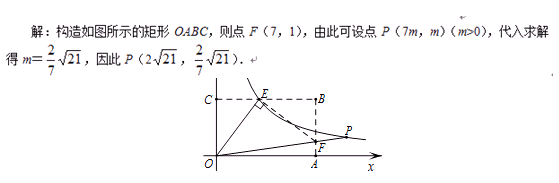
这里求出F（7,1），知tan∠FOA=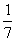，P在射线OF上，所以增量巧设P点左标为（7m,m）,将其代入解析式即可。

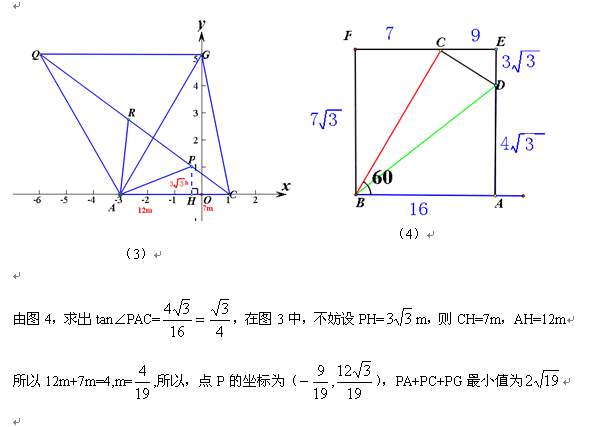
现在我们再回过头来看南通的这道中考题：

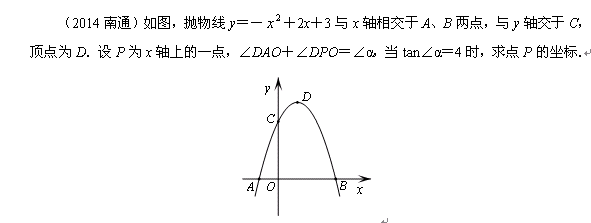
现在看到 “∠DAO＋∠DPO＝∠α，”这个条件，有想法了吗？

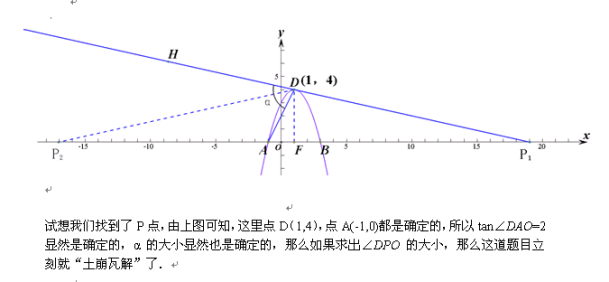
根据∠DPO=∠α－∠DAO现在估计很多朋友在“施法”框矩形了！

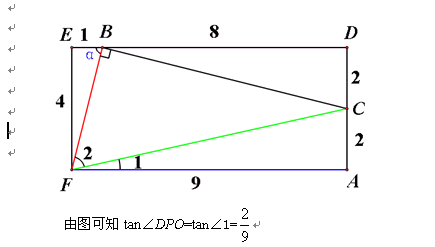
而DF=4，所以FP=18，所以P点坐标为（19,0）或（-17,0）
如果在原图外另构图的话，那是不是分分钟的事情呢！

即使我们不向学生介绍这种方法，作为教师掌握了这个“大法”，当学生来问你题时，你能快速地报出答案，那学生岂不对你佩服的五体投地呢！

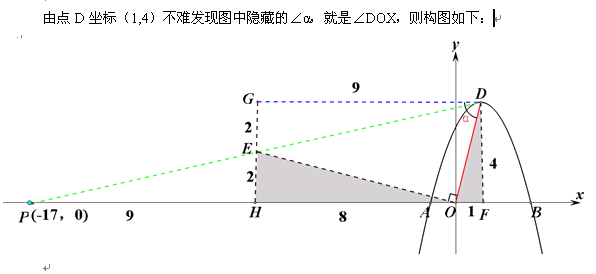
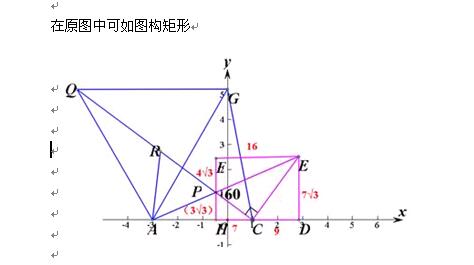
在原图上就可以如上构图

利用平行关系可知∠GDO=∠DOX=tanα=4，在∠GDO内部过点O作垂线构造tan∠EDO=tan∠DAO=2的直角三角形,所以两阴影的三角形的相似比为1:2，则可表示出矩形FDGH边上各部分线段长，可得P点坐标为（-17,0）再根据对称性得另一点坐标（19,0）

除了这种矩形构造，我们还可以构造更具一般性的矩形。

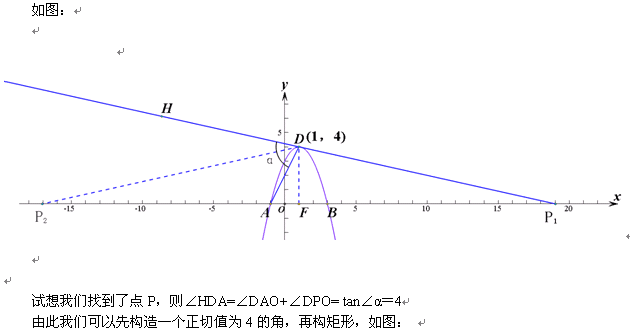
本想静静地学习，发现实在不行。黄萍老师是一位优秀的数学老师，其他老师能否静静聆听讲解呢？您上课讲的时候学生也讲，有何效率？有问题能否课后问？得罪了。

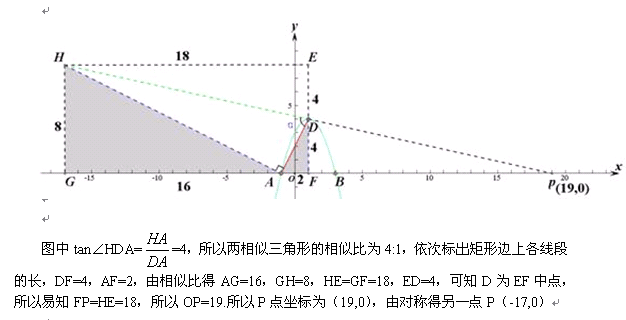
这里由于题中D点的坐标特征，利用tan∠DOF=4，命题人存在构思巧妙的方法
倘若我们没有发现这一点呢？

但这里用“矩形大法”，我们可以无视这个条件
譬如把“tan∠α＝4”改成3

也许原先的巧妙构思就不再可以了，而“矩形大法”在此可再显其神威

无论怎么变，只要两角的值是确定的，都可以“强行破门”，“直接碾压”．
大家可以一试

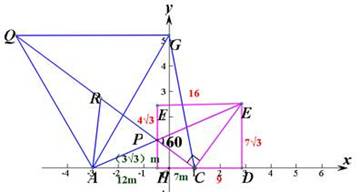
其实只要在上图中改动几个数据即可：
图中tan∠HDA=3，所以两相似三角形的相似比为3:1，依次标出矩形边上各线段的长就OK了！P(-27,0)或（29,0）

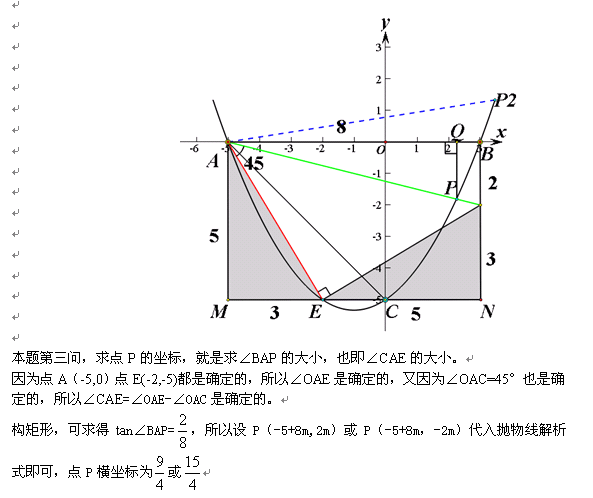
7、再来破解今年盐城的这题：

、
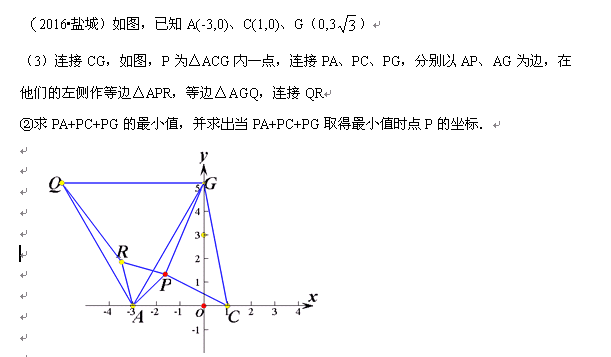
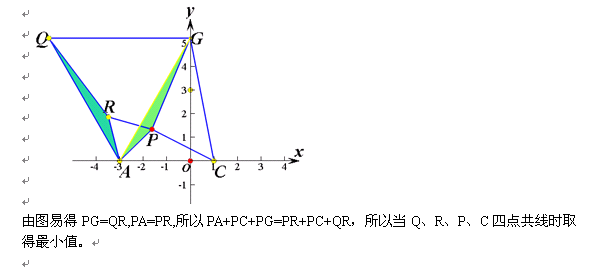
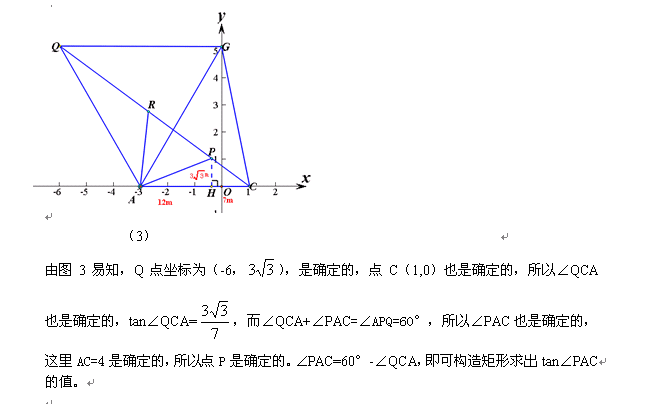
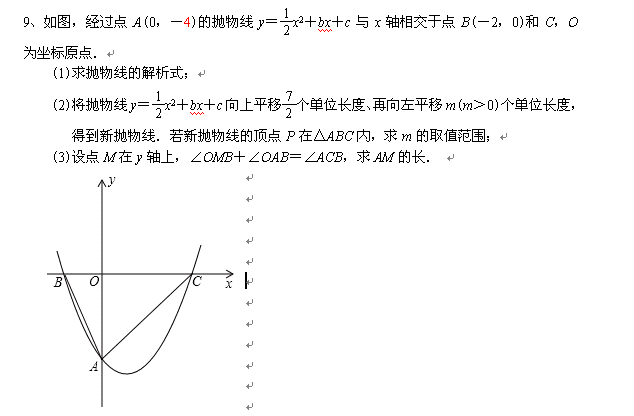