17.单线段最值问题（一）——基本分类

                                 八九年级全等与旋转模型归纳

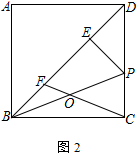
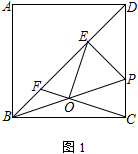
考察点1：手拉手模型

手拉手模型，亦称为共顶点等腰型，一定会出现旋转型全等。

其衍生模型有等腰对补角模型和等腰旁等角模型

模型回顾：

一 . 绕点旋转

.

.

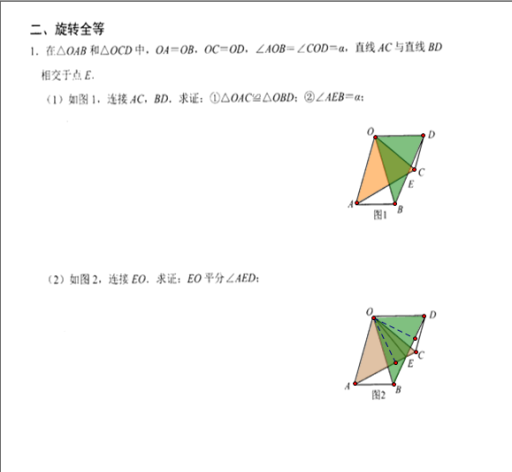
三．等腰旁等角型

.

.

.

.

四 等腰对补角型

.

.

.

.

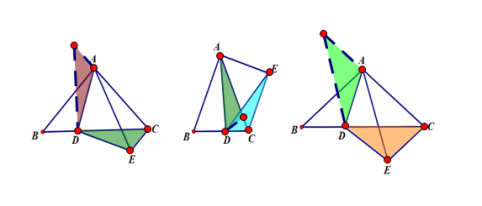
考察点2：”脚拉脚”模型。构造辅助线思路是先中线倍长，再证明旋转全等。

如图AB=AC，CD=ED，∠BAC+∠CDE=180°，若P为BE中点，求证：

.

.

.

.

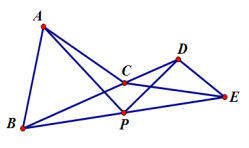
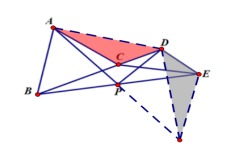
如图，∠A+∠C=180°，E，F分别在BC,CD上，且AB=BE，AD=DF，M为EF中点，求证：DM⊥BM

.

.

.

      

.

.

.

.

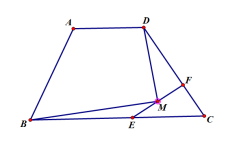
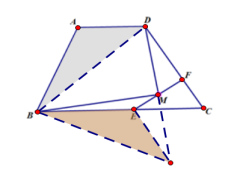
巩固练习

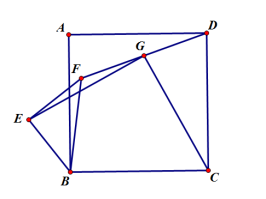
如图，已知等边△ABC，D是BC上任意一点，以AD为边作等边△ADE，连CE，求证：（1）CD+CE=AC，（2）CE是△ABC的外角平分线.

.

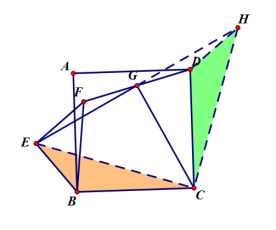
如图，已知△ABC，以AB、AC为边作正△ABD和正△ACE，CD交BE于O，连OA，求的值.

.

.

      

.

.

                    

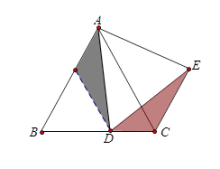
(1) 如图1，AB＝AC， D为BC上一点，DA＝DE，∠BAC=∠ADE＝90°，

求∠BCE的度数．

(2) 如图2，AB=AC，D为BC上一点，DA＝DE，∠BAC＝∠ADE = α°（α<90），

求证: AB // CE

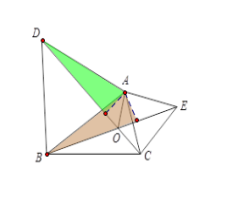
(3) 如图3，若△ABC和△ADE都是钝角三角形，那么（2）中结论是否变化 ？

.

.

.

.

.

.

.

.

.

.

.

.

.

.

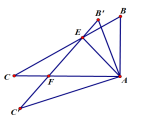
5，如图△ABC和△CDE均为等腰直角三角形，D为AB上一点，若∠ADE=15°，

M为BE中点，DM=，试求AC长度。

.

.

.

.

.

.

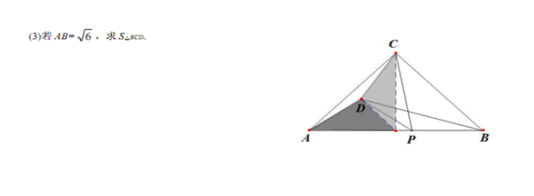
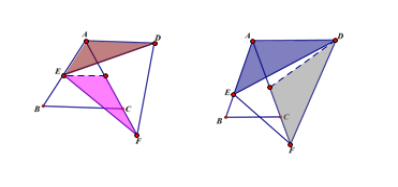
如图1，等边三角形ABC和等边三角形DEC，CE和AC重合

(1) 求证：AD＝BE

(2) 当CD＝AC时，若CE绕点C顺时针旋转30°，连BD交AC于点G，取AB的中点F连FG（如图2），求证：BE＝2FG

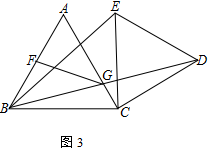(3) 在(2)的条件下AB＝2，则AG＝__________（直接写出结果）

.

.

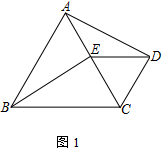
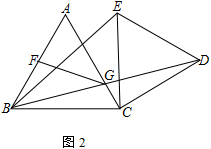
正方形中的旋转问题

6.如图，四边形ABCD、BEFG均为正方形

(1) 如图1，连接AG、CE，试判断AG和CE的数量关系和位置关系并证明

(2) 将正方形BEFG绕点B顺时针旋转β角（0°＜β＜180°），如图2，连接AG、CE相交于点M，连接MB，求∠EMB的度数

(3) 若BE＝2，BC＝6，连接DG，将正方形BEFG绕点B顺时针旋转β角（0°＜β＜180°），则在这个旋转过程中线段DG的取值范围为_______________（直接填空，不写过程）

.

.

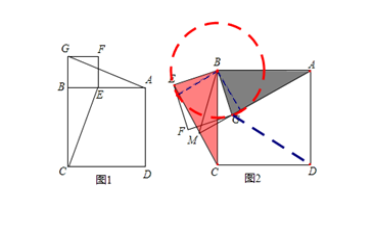
半角模型加强

原题呈现：

半角模型，又称为夹半角模型，半角旋转模型。常用辅助线做法，旋转或折叠。其中核心处理思路是通过几何变换把图形条件转化和集中，从而找到问题的突破口

举一反三：

（2017原创）

.

(武汉中考2017)如图，在△ABC中，AB＝AC＝，∠BAC＝120°，点D、E都在边BC上，

∠DAE＝60°．若BD＝2CE，则DE的长为___________．

                                                                      

.

.

.

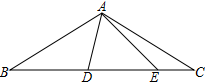
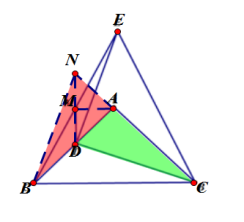
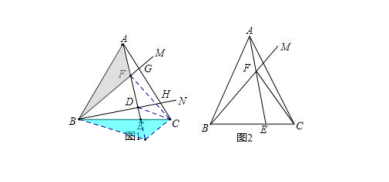
已知在△ABC中，AB=AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H

如图1，若∠ABC=60°、∠MBN=30°，作AE⊥BN于点D，分别交BC、BM于点E、F①求证：CE=AG；

②若BF=2AF，连接CF，求∠CFE的度数；

（2）如图2，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE=∠BAC=2∠CFE，直接写出=　　　　　　．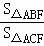

.

.

（硚口九月2017）在正方形ABCD中，AB＝6，P为边CD上一点，过P点作PE⊥BD于点E，连接BP. O为BP的中点，连接CO并延长交BD于点F.

.

.

.

.

.

.