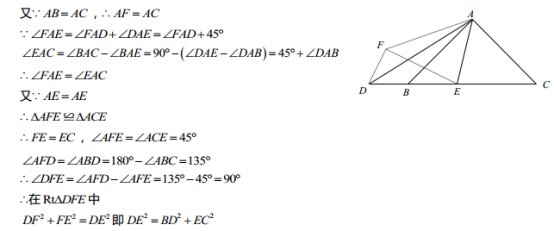15.半角模型
半角模型
模型 倍长中线或类中线(与中点有关的线段)构造全等三角形
已知如图:
∠2=∠AOB,OA=OB。
连接FB,将△FOB绕点O旋转
至△F′OA的位置,连接F′E、FE,
可得△OEF′≌△OEF。
基本模型(1)——正方形内含半角
如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。
![2c7dc1d5[1]](https://edu.data-discovery.cn/wp-content/uploads/2023/08/%E5%9B%BE%E7%89%87-45.png)
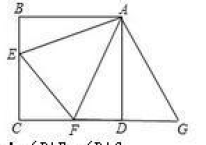
基本模型(2)——等边三角形内含半角


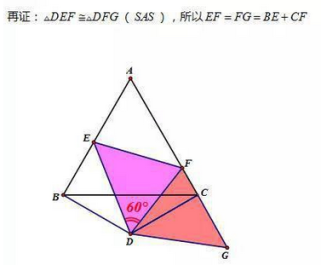
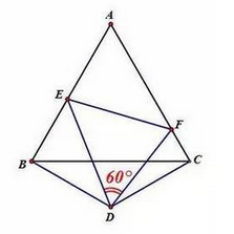
基本模型(3)——等腰直角三角形内含半角
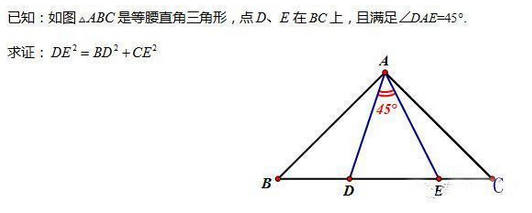
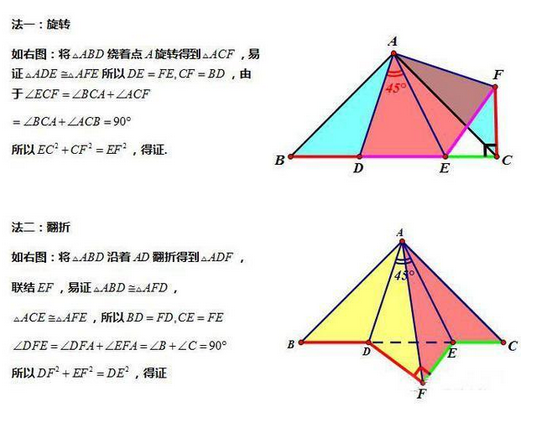
模型分析
(1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点;
(2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系;
(3)常见的半角模型是90°含45°,120°含60°。
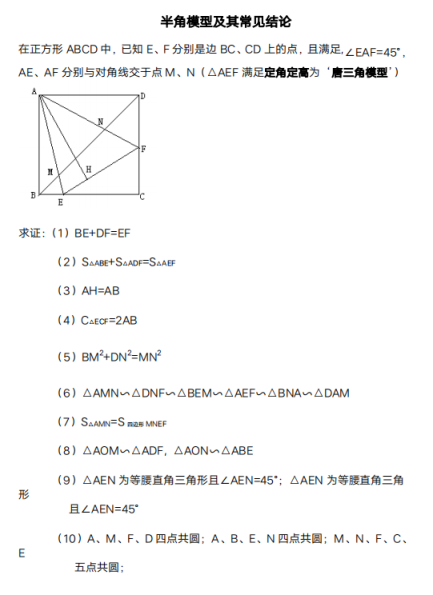
核心母题 如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF.
![2c7dc1d5[1]](https://edu.data-discovery.cn/wp-content/uploads/2023/08/%E5%9B%BE%E7%89%87-34-1.png)

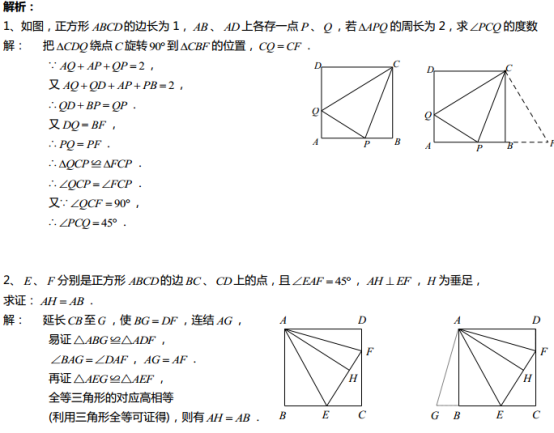
变式一:如图,E、F分别是边长为 1的正方形ABCD的边BC、CD上的点,若△ECF的周长是2,求∠EAF的度数?
![2c7dc1d5[1]](https://edu.data-discovery.cn/wp-content/uploads/2023/08/%E5%9B%BE%E7%89%87-33.png)

变式二:如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,AG⊥EF,求证:AG=AB.
![2c7dc1d5[1]](https://edu.data-discovery.cn/wp-content/uploads/2023/08/%E5%9B%BE%E7%89%87-32-1.png)

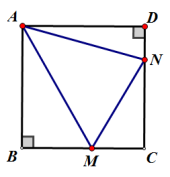
综合:在正方形ABCD中,若M、N分别在边BC、CD上移动,且满足MN=BM +DN,
求证:①.∠MAN=②.
③.AM、AN分别平分∠BMN和∠DNM.
练习
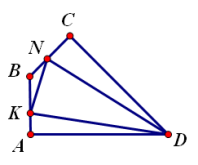
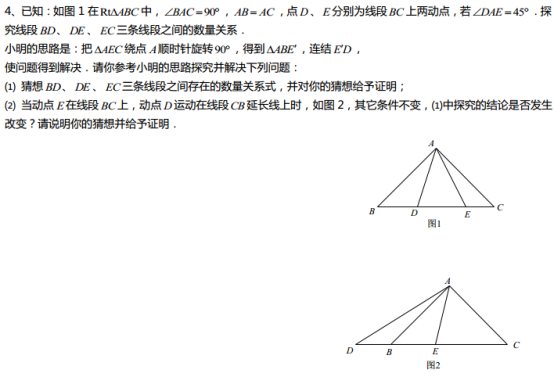
(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
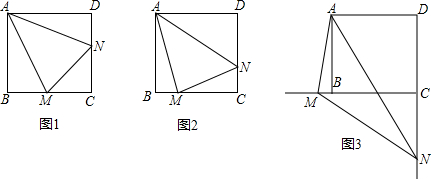


3、如图,在四边形ABCD中,AB=AD,,∠B+∠D=180°,E、F分别是边BC、CD上的点,且2∠EAF=∠BAD,
![c5eba628[1]](https://edu.data-discovery.cn/wp-content/uploads/2023/08/%E5%9B%BE%E7%89%87-26.png)
![f99f9fbf[1]](https://edu.data-discovery.cn/wp-content/uploads/2023/08/%E5%9B%BE%E7%89%87-25.png)
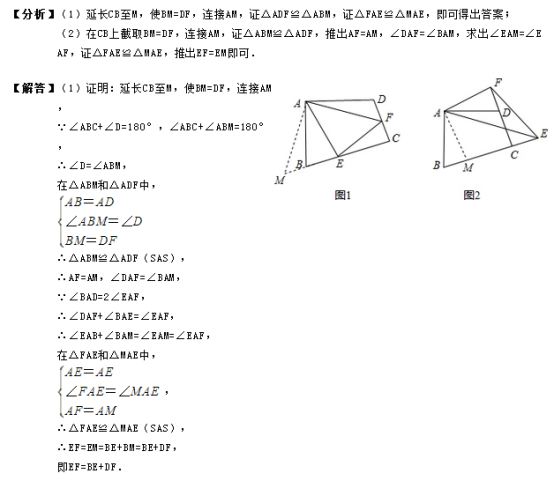

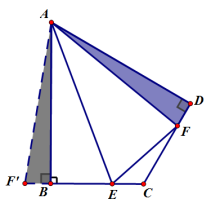
4、如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°求证:AD平分∠CDE.
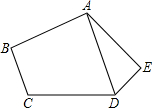

5、如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边形ABCDE的面积.
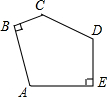

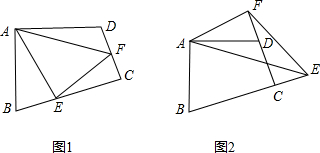
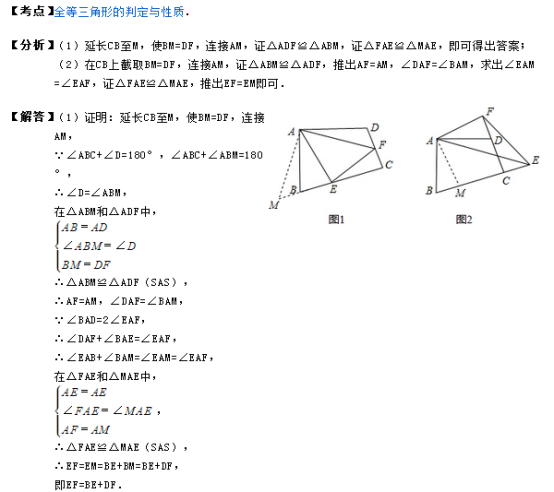
6、如图1.在四边形ABCD中.AB=AD,∠B+∠D=180゜,E、F分别是边BC、CD上的点,且∠BAD=2∠EAF.
(1)求证:EF=BE+DF;
(2)在(1)问中,若将△AEF绕点A逆时针旋转,当点E、F分别运动到BC、CD延长线上时,如图2所示,
试探究EF、BE、DF之间的数量关系.

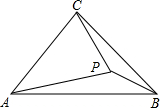
7、如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PC=2,PB=1.求∠BPC的度数

半角模型
条件:
思路:
(1)、延长其中一个补角的线段
(延长CD到E,使ED=BM ,连AE或延长CB到F,使FB=DN ,连AF )
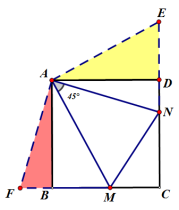 结论:①MN=BM+DN ②
结论:①MN=BM+DN ② ③AM、AN分别平分∠BMN和∠DNM
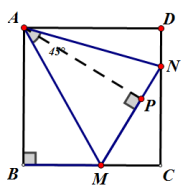
思路:分别将△ABM和△ADN以AM和AN 为对称轴翻折,但一定要证明
M、P、N三点共线.(∠B+∠D=且AB=AD)
例题应用:例1、在正方形ABCD中,若M、N分别在边BC、CD上移动,且满足MN=BM +DN,求证:①.∠MAN=
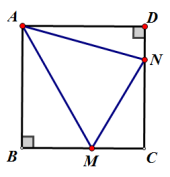 ②.
②.
③.AM、AN分别平分∠BMN和∠DNM.
思路同上略.
例1拓展:在正方形ABCD中,已知∠MAN=,若M、N分别在边CB、DC的延长线上移动,
①.试探究线段MN、BM 、DN之间的数量关系.
②.求证:AB=AH.
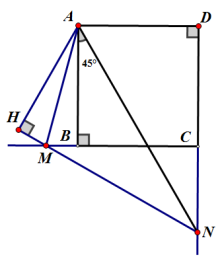 提示如图:
提示如图: 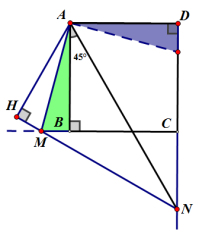
例2.在四边形ABCD中,∠B+∠D=,AB=AD,若E、F分别在边BC、CD上,且满足EF=BE +DF.求证:
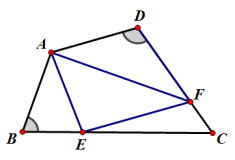 提示:
提示: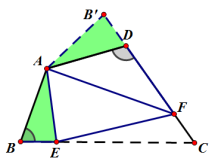
练习巩固:如图,在四边形ABCD中,∠B=∠D=,AB=AD,若E、F分别在边BC、CD 上的点,且
. 求证:EF=BE +DF.
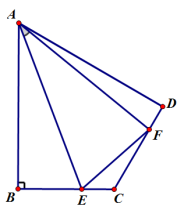 提示:
提示: