14.中点四大模型

模型 1 倍长中线或类中线（与中点有关的线段）构造全等三角形

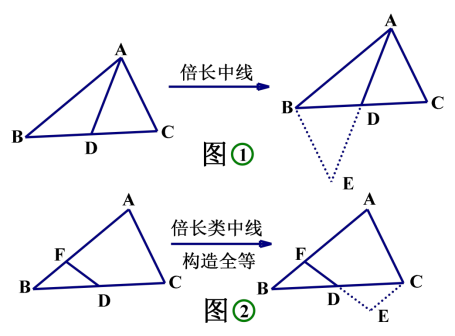
模型分析

如图①，AD是△ABC 的中线，延长AD至点E 使 DE=AD，易证：△ADC≌△EDB（SAS）。

如图②，D 是 BC 中点，延长 FD 至点 E 使 DE=FD，易证：△FDB≌△FDC（SAS）。当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移。

.

.

模型实例

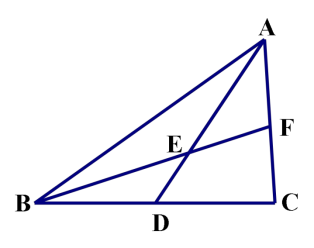
例 1．如图，已知在△ABC中，AD是BC边上的中线，E 是 AD 上一点，连接BE并延长AC于点F，AF=EF。求证：AC=BE。

.

.

模型精练

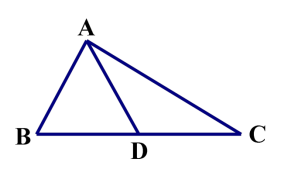
1．如图，在△ABC 中，AB=12，AC=20，求 BC 边上中线 AD 的范围。

.

.

.

.

.

.

.

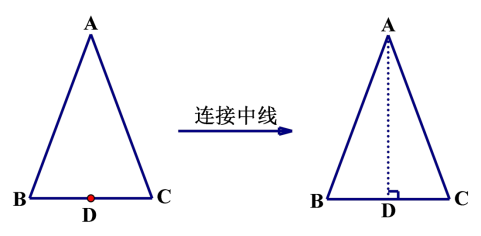
模型 2 已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”

.

.

.

模型分析

等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等或边相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到：“边等、角等、三线合一”。

.

.

模型实例

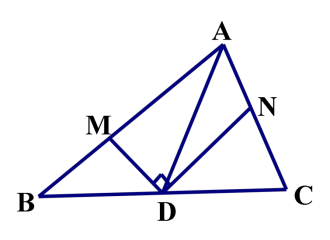
例 1．如图，在△ABC 中，AB=AC=5。BC=6，M为BC的中点，MN⊥AC 于点 N，求 MN 的长度。

.

.

模型精练

求证：∠EDB=∠FDC。

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

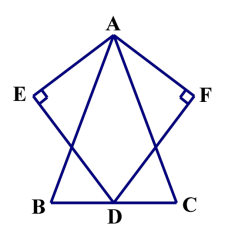
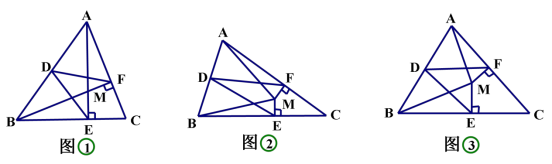
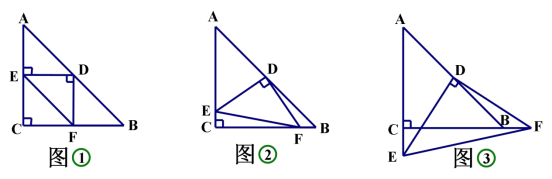
∠EDF=90°，∠EDF 绕点 D 旋转，它的两边分别交 AC、CB（或它们的延长线）于 E、F。

（1）当∠EDF 绕点 D 旋转到 DE⊥AC 于 E 时（如图①），

求证： SDEF +SCEF =1/2 SABC ；

（2）当∠EDF 绕点 D 旋转到 DE 和 AC 不垂直时，在图②和图③这两种情况下,上述结论是否成立？若成立，请给予证明；若不成立， SDEF 、SCEF 、SABC 又有怎样的数量关系？请写出你的猜想，不需证明。

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

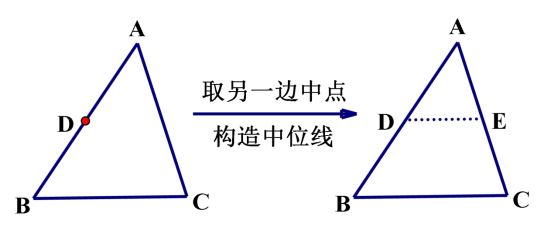
模型 3 已知三角形一边的中点，可以考虑中位线定理

.

.

.

.

.

.

.

.

模型分析

在三角形中，如果有中点，可构造三角形的中位线，利用三角形中位线的性质定理：DE∥BC，且 DE =1/2 BC 来解题，中位线定理既有线段之间的位置关系又有数量关系，该模型可以解决相等，线段之间的倍半、相等及平行问题。

.

.

.

.

.

.

.

模型实例

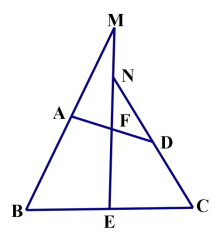
例 1．如图，在四边形 ABCD 中，AB=CD，E、F 分别是 BC、AD 的中点，连接EF并延长，分别与 BA、CD 的延长线交于点 M、N。

求证：∠BME=∠CNE。

.

.

.

.

.

.

.

.

.

.

.

.

模型精练

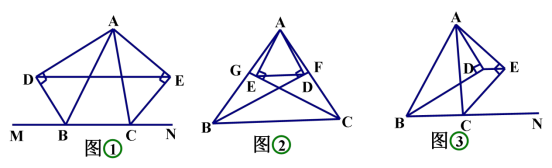
1．（1）如图①，BD、CE 分别是△ABC 的外角平分，过点 A 作 AD⊥BD、AE⊥CE，垂足分别为 D、E，连接 DE。

求证：DE∥BC， DE =1/2 (AB+BC+AC) ；

（2）如图②，BD、CE 分别是△ABC 的内角平分，其它条件不变。上述结论是否成立？

（3）如图③，BD 是△ABC 的内角平分，CE 是△ABC 的外角平分，其它条件不变。DE 与 BC 还平行吗？它与△ABC 三边又有怎样的数量关系？请写出你的猜想，并对其中一种情况进行证明。

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

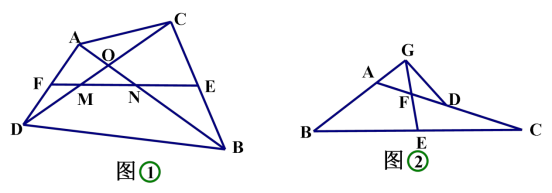
2．问题一：如图①，在四边形 ACBD 中，AB 与 CD 相交于点 O，AB=CD，E、F分别是 BC、AD 的中点，连接 EF 分别交 DC、AB 于点 M、N，判断△OMN 的形状，请直接写出结论；

问题二：如图②，在△ABC 中，AC>AB，点 D 在 AC 上，AB=CD，E、F 分别是 BC、AD 的中点，连接 EF 并延长，与 BA 的延长线交于点 G，若 ∠EFC=60°，连接 GD，判断△AGD 的形状并证明。

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

模型 4 已知直角三角形斜边中点，可以考虑构造斜边中线

.

.

.

.

模型分析

在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直角三角形斜边上的中线等于斜边的一半，即CD =1/2 AB ，来证明线段间的数量关系，而且可以得到两个等腰三角形：△ACD 和△BCD，该模型经常会与中位线定理一起综合应用。

.

.

.

.

.

.

模型实例

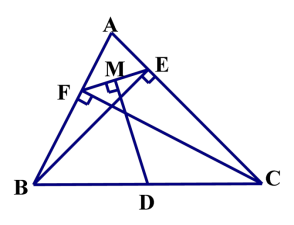
例 1．如图，在△ABC 中，BE、CF 分别为 AC、AB 上的高，D 为 BC 的中点，DM⊥EF 于点 M。求证：FM=EM。

模型精练

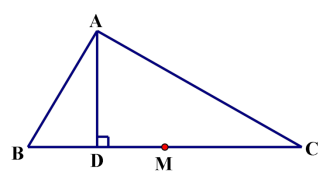
1．如图，在△ABC 中，∠B=2∠C，AD⊥BC 于点 D，M 为 BC 的中点，AB=10。

求 DM 的长度。

.

.

2．已知，△ABD 和△ACE 都是直角三角形，且∠ABD=∠ACE=90°，连接 DE，M 为 DE 的中点，连接 MB、MC。求证：MB=MC。

.

.

3．问题 1：如图①，△ABC 中，点 D 是 AB 边的中点，AE⊥BC，BF⊥AC，垂足分别为点 E、F，AE、BF 交于点 M，连接 DE、DF。若 DE =kDF ，则k 的值为_____；

问题 2：如图②，△ABC 中，CB=CA，点 D 是 AB 边的中点，点 M 在△ABC 内部，且∠MAC=∠MBC。过点 M 分别作 ME⊥BC，MF⊥AC，垂足分别为点 E、F，连接 DE、DF。若 DE=DF；

问题 3：如图③，若将上面问题②中的条件“CB=CA”变为“CB≠CA”，其它条件不变，试探究 DE 与 DF 之间的数量关系，并证明你的结论。