13.蚂蚁行程

模型 1 立体图形展开的最短路径

模型分析

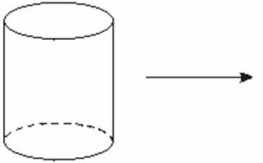
上图为无底的圆柱体侧面展开图，如图蚂蚁从点 A 沿圆柱表面爬行一周，到点 B 的最短路径就是展开图中 AB′的长。做此类题目的关键就是，正确展开立体图形，利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。

模型实例

例 1．有一圆柱体油罐，已知油罐底面周长是 12m，高 AB 是 5m，要从点 A 处

开始绕油罐一周建造房子，正好到达 A 点的正上方 B 处，问梯子最短有多长？

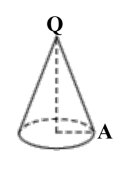
例 2．如图，一直圆锥的母线长为 QA=8，底面圆的半径r =2，若一只小蚂

蚁从 A 点出发，绕圆锥的侧面爬行一周后又回到 A 点，则蚂蚁爬行的最短

路线长是多少？

例 3．已知长方体的长、宽、高分别为 30cm、20cm、10cm，一只蚂蚁从 A

处出发到 B 处觅食，求它所走的最短路径。（结果保留根号）

模型练习

1．有一个圆锥体如图，高 4cm，底面半径 5cm，A 处有一蚂蚁，若蚂蚁欲沿侧

面爬行到 C 处，求蚂蚁爬行的最短距离。

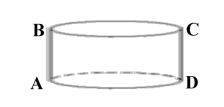
2．如图，圆锥体的高为 8cm，底面周长为 4cm，小蚂蚁在圆柱表面爬行，从 A

点到 B 点，路线如图，则最短路程是多少？

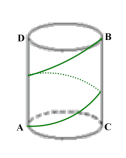
3．桌上有一个圆柱形无盖玻璃杯，高为 12 厘米，底面周长 18 厘米，在杯口

内壁离杯口距离 3 厘米的 A 处有一滴蜜糖，一只小虫 22 杯子外壁，当它

正好在蜜糖相对方向离桌面 3 厘米的 B 处时，突然发现了蜜糖，问小虫至

少爬多少厘米才能到达蜜糖所在的位置。

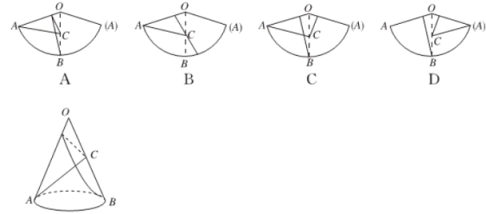
4．已知 O 为圆锥顶点，OA、OB 为圆锥的母线，C 为 OB 的中点，一只小蚂蚁

从点 C 开始沿圆锥侧面爬行到点 A，另一只小蚂蚁也从 C 点出发绕着圆锥

侧面爬行到点 B，它们所爬行的最短路线的痕迹如图所示，若沿 OA 剪开，

则得到的圆锥侧面展开图为（）

1572850134(1)

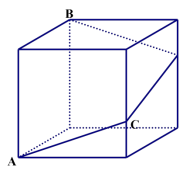
5．如图，一只蚂蚁沿着边长为 2 的正方体表面从点 A 出发，经过 3 个面爬行

到点 B，如果它运动的路径是最短的，则最短距离为多少？

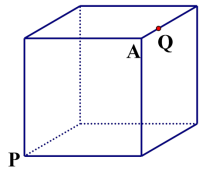
6．如图是一个边长为 6 的正方体木箱，点 Q 在上底面的棱上，AQ=2，一只

蚂蚁从 P 点出发沿木箱表面爬行到点 Q，求蚂蚁爬行的最短路线。

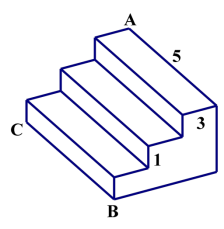
7．如图，是一个三级台阶，它的每一级的长、宽和高分别等于 5cm、3cm 和

1cm，A 和 B 是这个台阶的两个相对的端点，A 点上有一只蚂蚁，想到 B 点

去吃可口的食物。请你想一想，这只蚂蚁从 A 点出发，沿着台阶面爬到 B

点的最短路程是多少？