10.一线三等角模型
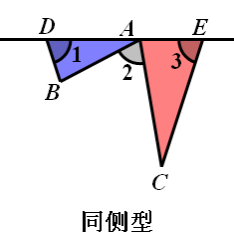
“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形。这个角可以是直角,也可以是锐角或者钝角。对于“一线三等角”,有的地区叫“K型图”,也有的地区叫“M型图”。
“一线三等角”的起源
DE 绕 A 点旋转,从外到内,从一般位置到特殊位置.

下面分几种类型讨论:
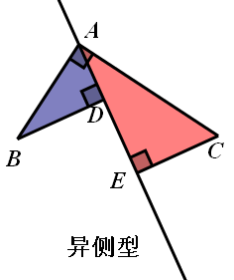
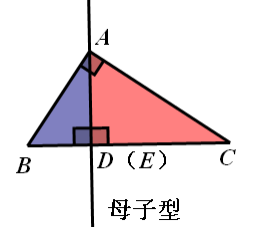
一、直角形“一线三等角”——“一线三直角”
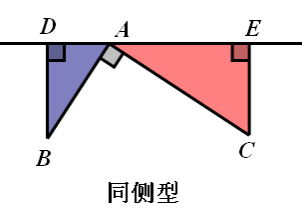
结论:△ADB ∽△CEA
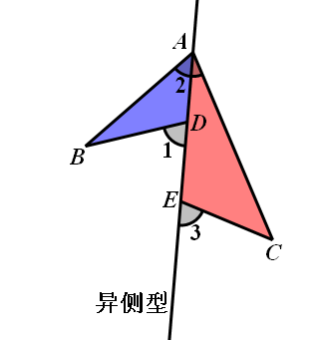
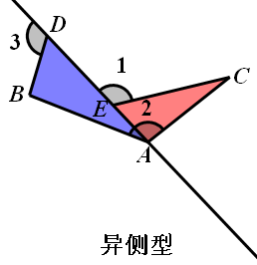
结论:△ADB∽△CEA∽△CAB
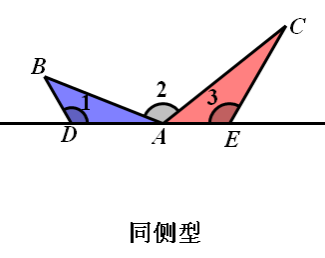
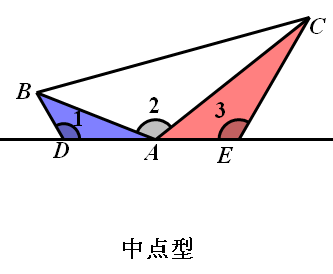
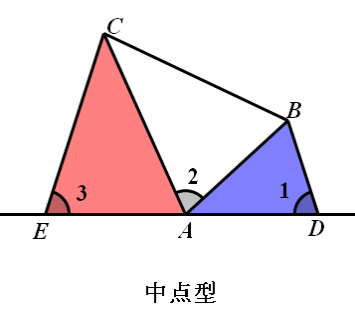
结论:△ADB∽△CEA∽△CAB
下面总结几种常考类型:
类型一 三角齐见,模型自现
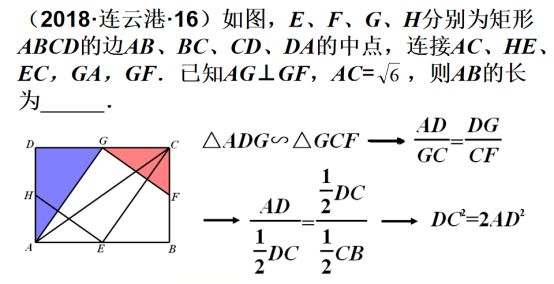
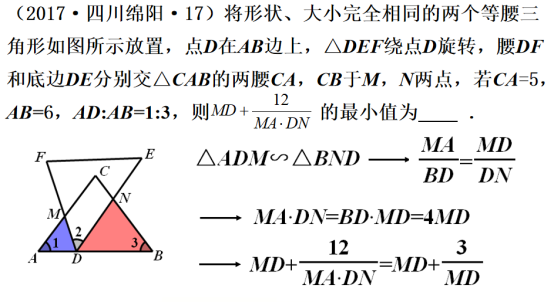
类型一概述
以上两例都是典型的“一线三等角”试 题,由于模型的框架已搭建,因此降低了试题的起 点. 两道题虽涉及不同的图形变换,但解法本质一 致,均为利用模型构建比例式解决问题. 两道题都 着重考查学生在图形变换过程中的观察理解、直观 感知、推理转化等数学能力和思想.
类型二 隐藏局部,小修小补
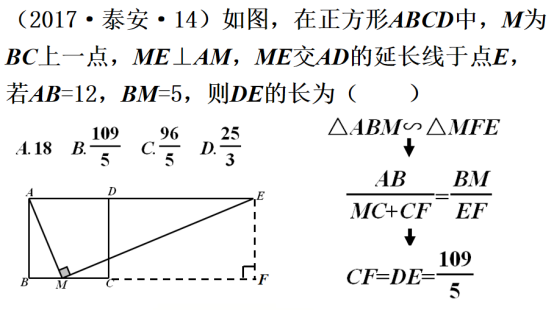

类型二概述
上述两道题虽分别以四边形和一次函数为命题背景,但图形的共性较明显: 均将原有 “一线三等角”模型中的一角进行了隐藏,而这就要求学生理性地从图形的角度进行思考与联想,发现其中最本质的特征,挖掘蕴含在图中的几何模 型.两道题均较好地体现了对“四基”的综合考查, 提升了学生思维的层次性和灵活性.
类型三 一角独处,两侧添补


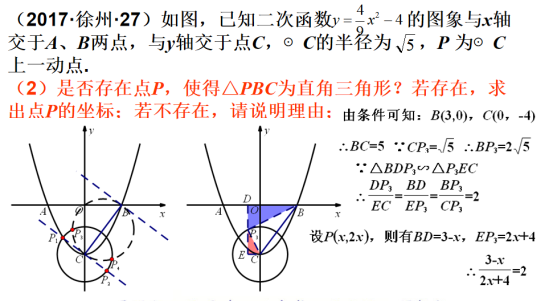
类型三概述
上述几道题虽呈现的背景不同,但都蕴 知识技能、思想方法、数学模型于图形之中.题中的 “特殊角”是解题的关键,也是搭建模型框架的基础,更是学生解题思路的来源与“脚手架”. 这几道题实质上都是考查学生利用模型进行数学思考的能力,同时也有效地检测了学生对数学本质属性的把握情况.
类型四 线角齐藏,经验来帮

类型四概述
本题实质上以图形的旋转为问题的切入点,较好地激发学生探索的意愿,促使学生在模拟图形运动的同时,自发地利用题中所 蕴含的特殊角,展开适当的联想,寻找图形间的联系,利用数学解题经验,搭建模型框架。本题意在寻求突破,体现分层考查,有着较好的考试信度与效度.
通过上述四种应用类型的后三种,我们不难发现:对于有些中考试题,“一线三等角”并非直观、完整地呈现,而是在原图中隐藏了局部或全部结构,因此思维层次随之提升。若我们能充分利用题中所给的已知角或挖掘图中隐藏的特殊角,通过“找角,定线,搭框架”,让模型“现出原形”,则解题思路便会油然而生,豁然开朗。
在近几年的各地中考试卷中,逐渐涌现出由同一类基本模型延伸而来的试题,这些试题虽呈现的背景不尽相同,但解决问题的方法和思想相通,这就要求教师在平时的解题教学中,充分挖掘习题的内在价值,鼓励学生对问题进行深入研究,引导并总结出一般化的方法,同时要让学生尝试利 用在解题过程中所积累的经验,对试题中所蕴藏的基本模型进行挖掘与提炼.只有让学生学会自主地反思、推进、提炼,才能做到“掌握模型,举一反三,通一类题”,同时通过对一些基本模型和结论的挖 掘,能更好地弄清问题的本质,为解决问题搭建好思维的“脚手架”,进而切实有效地提升学生的解题能力,发展学生的思维水平.
